首页 > 算法 > 【算法】根据遍历结果还原二叉树

【算法】根据遍历结果还原二叉树

前面我们了解了二叉树的生成与遍历，并能得到正确的遍历结果。

此时我们不禁要想：能不能根据遍历结果（深度优先遍历）还原二叉树呢？

答案当然是肯定的，下面我们就探究一下。

方向分析

首先，能不能通过一个遍历结果确定唯一的二叉树？

答案是否定的，比如下图：

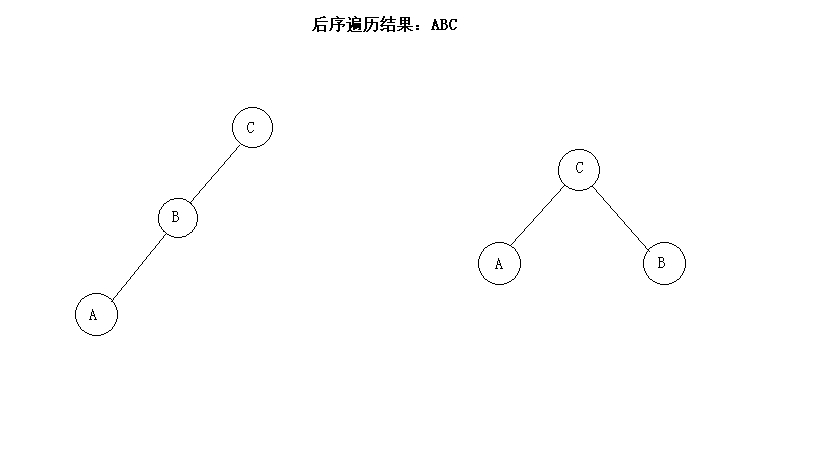
单单只通过前序、后序是无法确定一颗二叉树的，他们能确定节点的父子关系，但是缺失了节点间的兄弟关系；而中序遍历结果在确定根节点的情况下可以确定节点间的兄弟关系，在缺少根节点信息的情况下，无法确定父子关系。

既然通过一个遍历结果无法确定一棵二叉树，那么我们可不可以两两结合来判断？答案是可以的，因为“先序”、“后序”能确定二叉树的根节点和节点的父子关系，“中序”在根节点确定的情况下能确定节点的兄弟关系，所以“先序+中序”和“后序+中序”的组合能确定一颗二叉树，“先序+后序”的组合因为缺少节点兄弟关系故无法确定一棵树。

“先序+中序”分析及实现

如下图一颗二叉树

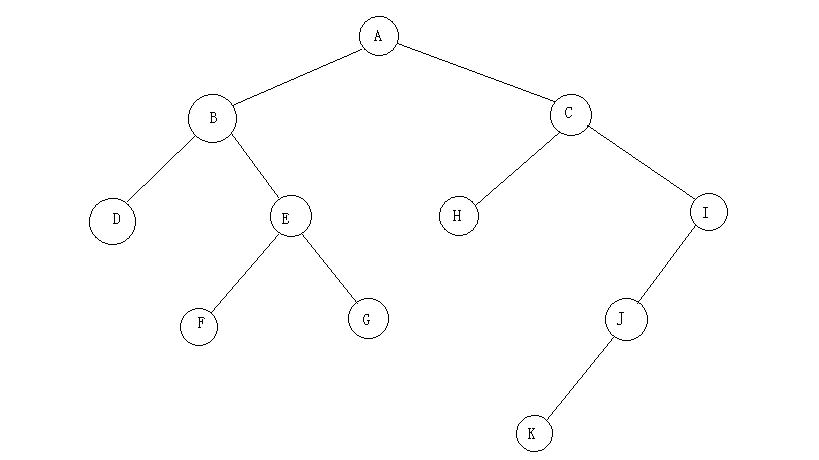
它的先序结果是：ABDEFGCHIJK，中序结果是：DBFEGAHCKJI，那么我们通过这两个结果的结合来还原这颗二叉树：

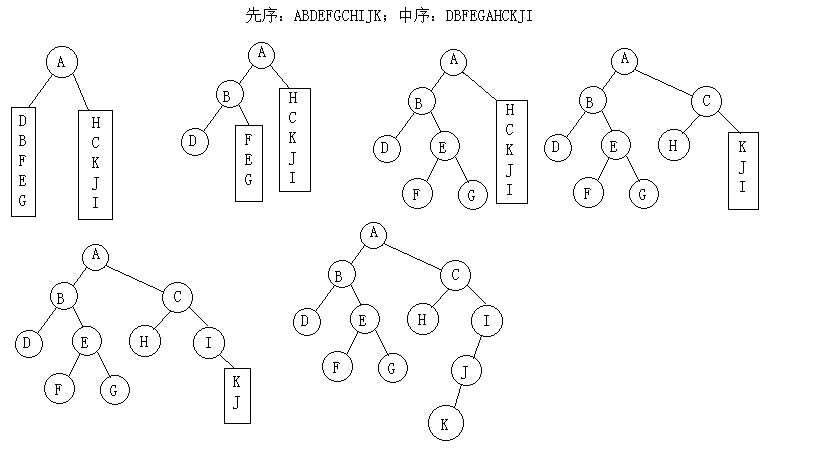
原理其实就是根据先序结果一层一层的确定根节点，然后根据中序结果判断左树和右树。下面我们用代码来实现一遍。

<!DOCTYPE html>
<html lang="en">
<head>
	<meta charset="UTF-8">
	<title>二叉树还原</title>
</head>
<body>
	<script>
		const DLR = ['A', 'B', 'D', 'E', 'F', 'G', 'C', 'H', 'I', 'J', 'K']
		const LDR = ['D', 'B', 'F', 'E', 'G', 'A', 'H', 'C', 'K', 'J', 'I']

		function restore(dlr = [], ldr = []) {
			let node
			const nodeValue = dlr.shift()
			const index = ldr.indexOf(nodeValue)
			if (index !== -1) {
				node = {}

				node.value = nodeValue;
				const ldr_left = ldr.slice(0, index);
				const dlr_left = dlr.filter(i => ldr_left.indexOf(i) !== -1)
				node.left = restore(dlr_left, ldr_left)

				const ldr_right = ldr.slice(index + 1);
				const dlr_right = dlr.filter(i => ldr_right.indexOf(i) !== -1)
				node.right = restore(dlr_right, ldr_right)
			}
			return node
		}

		console.log(restore(DLR, LDR))
	</script>
</body>
</html>

"后序+中序"分析及实现

其实和“前序+中序”一样，只不过根节点的位置在最后而不是一开始了，这里就不做另外分析说明了。

“前序+后序”分析

前面已经说明了，这两个遍历结果没有兄弟节点的关系信息，所以无法还原二叉树。